

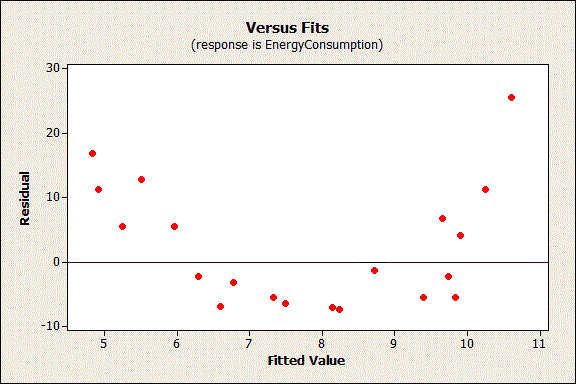
For example, a fitted value of 8 has an expected residual that is negative. In the graph above, you can predict non-zero values for the residuals based on the fitted value. Keep in mind that the residuals should not contain any predictive information. Now let’s look at a problematic residual plot. Therefore, the residuals should fall in a symmetrical pattern and have a constant spread throughout the range. Further, in the OLS context, random errors are assumed to produce residuals that are normally distributed. In other words, the model is correct on average for all fitted values. So, the residuals should be centered on zero throughout the range of fitted values. So, what does random error look like for OLS regression? The residuals should not be either systematically high or low. Just like with the die, if the residuals suggest that your model is systematically incorrect, you have an opportunity to improve the model.
#RESIDUAL ANALYSIS SERIES#
And, for a series of observations, you can determine whether the residuals are consistent with random error.
You shouldn’t be able to predict the error for any given observation. The same principle applies to regression models. His new mental model better reflects the outcome. If a gambler looked at the analysis of die rolls, he could adjust his mental model, and playing style, to factor in the higher frequency of sixes. If the number six shows up more frequently than randomness dictates, you know something is wrong with your understanding (mental model) of how the die actually behaves. However, you can assess a series of tosses to determine whether the displayed numbers follow a random pattern. When you roll a die, you shouldn’t be able to predict which number will show on any given toss. This process is easy to understand with a die-rolling analogy. Using residual plots, you can assess whether the observed error (residuals) is consistent with stochastic error. Statistical caveat: Regression residuals are actually estimates of the true error, just like the regression coefficients are estimates of the true population coefficients. If you observe explanatory or predictive power in the error, you know that your predictors are missing some of the predictive information. The idea is that the deterministic portion of your model is so good at explaining (or predicting) the response that only the inherent randomness of any real-world phenomenon remains leftover for the error portion. In other words, none of the explanatory/predictive information should be in the error. Putting this together, the differences between the expected and observed values must be unpredictable.
Error is the difference between the expected value and the observed value. Stochastic is a fancy word that means random and unpredictable. All of the explanatory/predictive information of the model should be in this portion. The expected value of the response is a function of a set of predictor variables. This is the part that is explained by the predictor variables in the model. Response = Deterministic + Stochastic The Deterministic Portion Response = (Constant + Predictors) + Error Why? To start, let’s breakdown and define the 2 basic components of a valid regression model: If you don’t have those, your model is not valid. The bottom line is that randomness and unpredictability are crucial components of any regression model. Have you ever wondered why? There are mathematical reasons, of course, but I’m going to focus on the conceptual reasons. Anyone who has performed ordinary least squares (OLS) regression analysis knows that you need to check the residual plots in order to validate your model.


 0 kommentar(er)
0 kommentar(er)
